USTC Achieves “Super-Heisenberg” and Heisenberg Scalings in Estimation of a Rotating Field Simultaneously
The research group led by Prof. LI Chuanfeng and Prof. XIANG Guoyong from CAS Key Laboratory of Quantum Information of the University of Science and Technology of China (USTC) of CAS, cooperated with Prof. YUAN Haidong from Chinese University of Hongkong, achieved “super Heisenberg scaling” and Heisenberg scaling simultaneously in the estimation of a rotating field for the first time. The result was published online in Physical Review Letters and was chosen as the PRL cover for this week.
The precision of quantum metrology can be increased by consuming more resources and is described as T-k , where T is the resource (i.g. time of evolution), and k is the order of the scaling. In many applications such as phase estimation, quantum magnetometry and quantum gyroscope, k is measured as 0.5 by classical method, and 1 by quantum method, which are known as ‘shot noise limit’ and ‘Heisenberg limit’, respectively.
However, in many-body interactions or time-dependent evolution, k can exceed 1, which is dubbed as ‘super-Heisenberg limit’. So far, these three precision limits have been achieved in single-parameter quantum estimation experiments, but it remains unclear whether the super-Heisenberg limit is really “super-Heisenberg” since the Heisenberg uncertainty relation is the fundamental limit in quantum mechanics.
To resolve this problem, Prof. XIANG’s group employed the platform of quantum precision measurement (Nat. Commun. 9,1(2018)) that’s been developed in recent years, and demonstrated that the precisions of the magnitude and frequency in a rotating field can simultaneously achieve the Heisenberg limit and super-Heisenberg limit, respectively. In this work, researchers developed and adapted the control-enhanced sequential scheme (PRL 123,040501(2019)) to measurement of multi-parameter time-dependent evolution. By optimizing each part in the evolution of the system, they realized optimal estimation where two parameters simultaneously achieved super-Heisenberg and Heisenberg scalings. It was clearly illustrated that both scalings saturated the Heisenberg uncertainty relation and achieved the highest quantum precision.
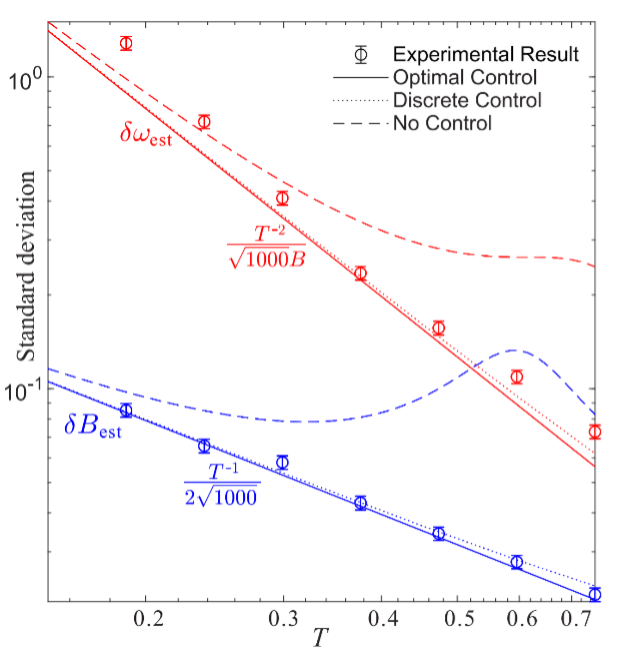
The precisions of frequency ω and magnitude B achieve super-Heisenberg and Heisenberg scalings respectively (Image by HOU Zhibo et al.)
As the first demonstration of simultaneously achieving two different Heisenberg scalings, this work deepens the understanding on the connection between the precision limit and the uncertainty relations, which sheds light on the studies of both fields and has wide implications in practical multi-parameter quantum estimation.
Paper link:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.070503
(Edited by LU Hongyu, USTC News Center)
Back
