A research group led by Prof. XU Ning from University of Science and Technology of China (USTC) of the Chinese Academy of Sciences (CAS), collaborating Prof. DENG Youjing, made progress in the research on the rigid percolation associated with the jamming transition. The study was published in Physical Review Letters.
Percolation refers to the process of a liquid moving gradually through a porous disordered medium. It happens when pores are randomly blocked to a certain degree so that the liquid stops flowing. Percolation in a thermodynamic equilibrium system is relatively fully studied whereas distinct behaviors in a nonequilibrium system still remain to be explained.
The jamming transition is a typical nonequilibrium solid-fluid transition. When the packing density of a large number of short-range interacting particles increases, nonrigid unbonded liquid will be converted to rigid blocked solid. For purely repulsive particles, rigidity in the jamming transition is discontinuous, presenting the characteristic of the first order transition.
However, attraction force is often exists in real systems, which may change the transition characteristic. Compared with purely repulsive systems, the study of attractive systems has more practical merits.
In this study, the researchers expanded the conventional perception that in the presence of attraction, the jamming transition corresponds to the rigidity percolation by discovering the abnormal rigidity percolation transition in a nonequilibrium system.
When the range of attraction is long, the jamming transition still exhibits behaviors similar to the rigidity percolation in an equilibrium system. The critical index is consistent to traditional hyperscaling relation. When the range of attraction is short, however, the distribution of the size of rigid clusters shows two distinct values, reflecting the largest cluster and the other cluster, respectively. Interestingly, in spite of the difference, these two type of clusters still have the same fractal dimension.
With the system’s expansion, two clusters both grow and tend to diverge in the thermodynamic size limit but in different growth rate. This indicates that there exists two length scales in an equilibrium system which is out of expectation since the single scale of the rigidity percolation.
In the framework of the two-scale scenario, the researchers derived a generalized hyperscaling relation to explain the deviation of hyperscaling brought by two distinct length scales. Researchers also proposed that as long as attractive forces exist, the percolation associated with the jamming transition is continuous. When attractive forces approaching zero, the characteristics of the jamming transition and a pure repulsive system are still intrinsically different.
The research provides new insights into the study of nonequilibrium system and has profound implications for the jamming transition.
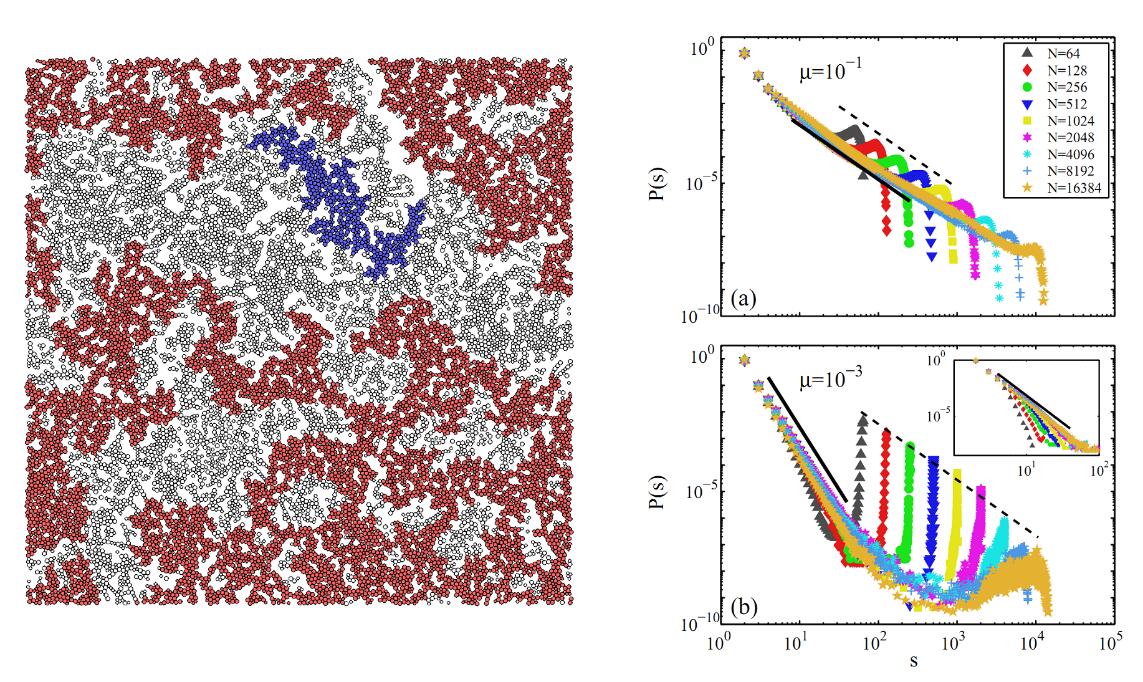
The left is the rigidity percolation of sticky particles. Red represents the largest rigid cluster and blue represents the second largest cluster. The right is the distribution P(s) of the size s of rigid clusters under the circumstances of long-rang attraction (a) and short-range attraction (b). Compared to the single distribution index shown in (a), two distinct indexes shown in (b) suggest two scales.
(Image by XU Ning et al.)
Paper link:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.255501
