Experimental Discovery of Weyl Semiconductors
Recently, the research team led by Prof. ZENG Changgan from University of Sciences and Technology of China (USTC), has revealed representative topological transport signatures of Weyl physics, and moreover, the logarithmically periodic quantum oscillations in the elemental semiconductor tellurium (Te), extending Weyl physics to semiconductor systems for the first time. The research article was published in PNAS on May 12th.
The recent discovery of Weyl fermions in solids enables exploitation of relativistic physics and the development of a spectrum of intriguing physical phenomena. From the viewpoint of material science, a Weyl point is just a two-fold band degeneracy, and therefore can in principle exist in any material satisfying the symmetry requirements. Until now, Weyl physics has been generally regarded as unique to semimetals, with the Weyl points located around the Fermi level. Nevertheless, considering the high tunability and compatibility with modern electronic industry, the semiconductor will be a better candidate material for designing topological electronic devices if exotic transport phenomena related to Weyl fermions can be realized.
Te is a narrow bandgap semiconductor possessing strong spin–orbit coupling, and it lacks space inversion symmetry due to the characteristic chiral crystal structure. The Weyl points are located near the valence band maximum, arising from the crossing of two spin-splitting bands. In this study, high-quality Te single crystals were grown via physical vapor deposition. The Fermi level resides in the valence bands due to the self-hole-doping characteristics of the as-grown crystals, thus enhancing the influence of Weyl fermions on the electrical transport behaviors. Via systematic magneto-transport measurements, the topological transport signatures of Weyl physics, e.g., the negative longitudinal magnetoresistance and the planar Hall effect, are observed. More strikingly, logarithmically periodic oscillations in both the magnetoresistance and Hall data are revealed beyond the quantum limit. The log-periodic oscillations originate from the formation of two-body quasi-bound states formed between Weyl fermions and opposite charge centers. The small Fermi velocity of Te crystals ensures the supercritical condition, promoting the formation of quasi-bound states with discrete scale invariance.
The present study reveals the topological nature of Te and further confirms the universality of discrete scale invariance in topological materials. Moreover, introduction of Weyl physics into semiconductors to develop “Weyl semiconductors” provides an ideal platform for manipulating fundamental Weyl fermionic behaviors and for designing future topological devices.
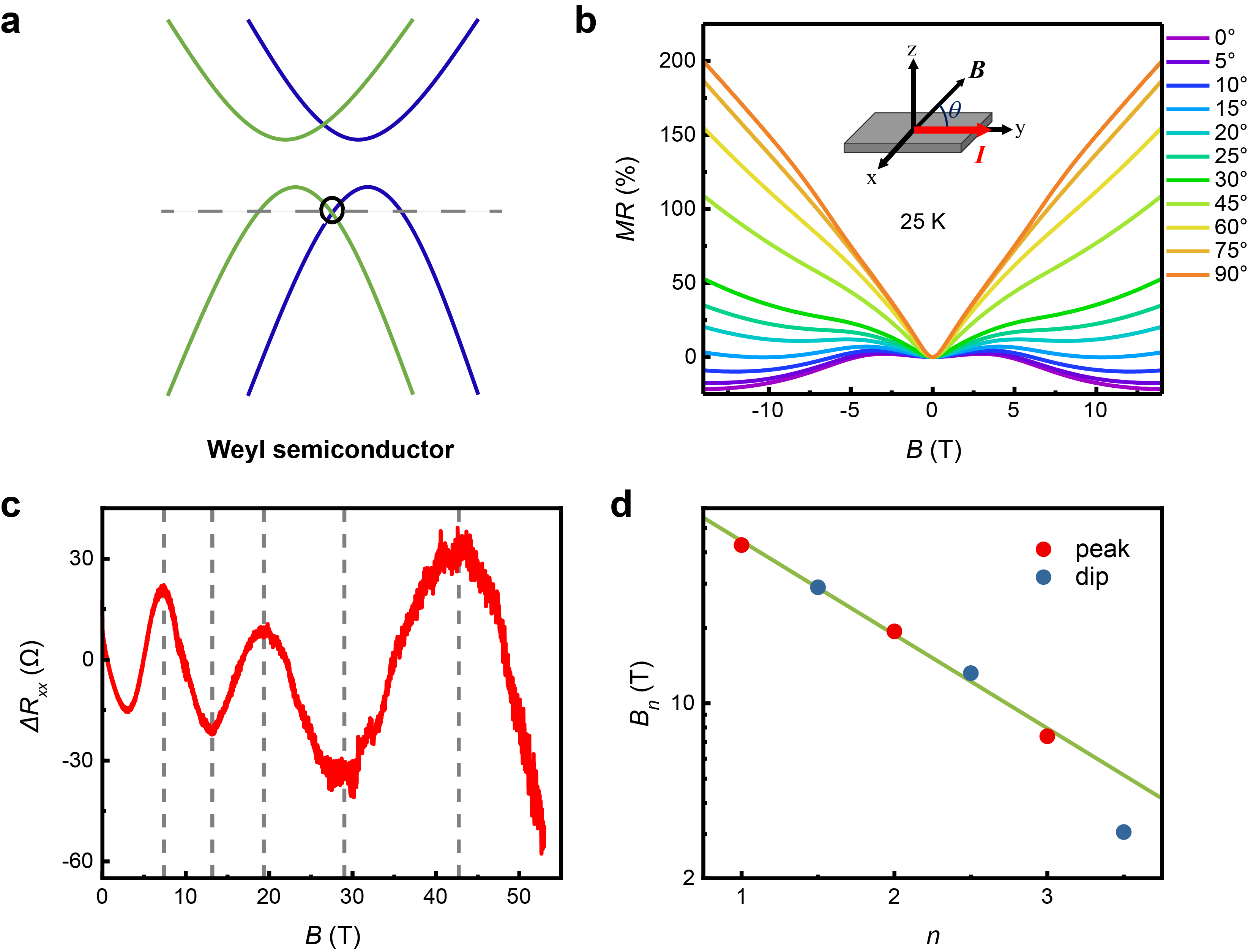
a, Schematic conceptual illustration of a Weyl semiconductor. The Weyl point is indicated by the black circle. b, Negative longitudinal magnetoresistance effect. c,d, Log-periodic magnetoresistance oscillations observed under strong magnetic fields.
Back
